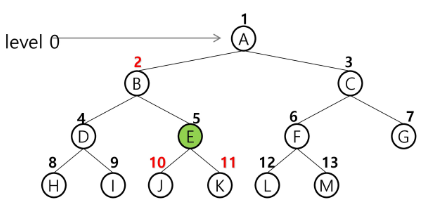
Tree - Binary Tree
트리란
비선형 구조
원소들 간 1:n관계를 가짐
계층형 자료구조
상위에서 하위로 내려가며 확장되는 구조

subtree : 루트를 제외하고 나머지 노드들은 분리 집합이 되며, 이를 루트의 부트리(subtree)라 함
node : 트리의 원소
edge(간선) : 노드를 연결하는 선. 부모 노드와 자식 노드를 연결
sibling node : 형제 노드. 같은 부모 노드의 자식 노드들 ex) B,C,D는 형제 노드
조상 노드 : 루트 노드까지 이르는 경로에 있는 모든 노드들 ex) K의 조상 노드 : F,B,A
자손 노드 : 서브 트리에 있는 하위 레벨의 노드들 ex) B의 자손 노드 : E,F,K
degree
- 노드의 차수 : 노드에 연결된 자식 노드의 수 ex) B의 차수:2, C의 차수:1
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값 ex) 트리 T의 차수 : 3
- 리프 노드(단말 노드) : 차수가 0인 노드. 자식 노드가 없는 노드
높이
노드의 높이 : 루트에서 노드에 이르는 간선의 수. 노드의 레벨 ex) B의 높이:1, F의 높이:2
트리의 높이: 가장 큰 노드의 높이. 최대 레벨 ex) 트리 T의 높이 : 3(K의 높이와 같음)
이진 트리
모든 노드가 2개의 서브트리를 갖는 트리
각 노드는 자식 노드를 최대 2개까지만 가질 수 있음 cf) left child node , right child node
레벨 i에서의 최대 노드 개수 : 2**i개
h+1 <= (높이가 h인 이진 트리가 가질 수 있는 노드 개수) <= 2**(h+1)-1

이진 트리의 종류
포화 이진 트리(Full Binary Tree)
모든 레벨에 노드가 포화상태로 차 있는 이진 트리
높이가 h일 때, 2**(h+1)-1 개의 노드를 가진 이진 트리

완전 이진 트리(Complete Binary Tree)
높이가 h, 노드 수가 n개 (2**h<=n<=2**(h+1)-1)
포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리

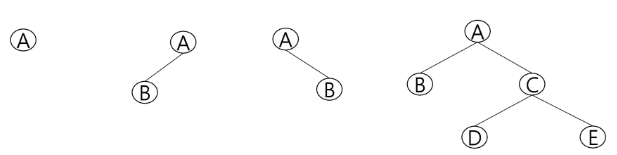
편향 이진 트리(Skewed Binary Tree)
높이 h에서 최소 개수의 노드를 가지며 한쪽 방향의 자식 노드만 가지는 이진 트리
왼쪽 편향, 오른쪽 편향이 있음
순회(traversal)

트리의 각 노드를 중복되지 않게 전부 방문하는 것
하지만, 비 선형 구조이기에 선형구조처럼 선후 연결 관계를 알 수 없음
순회 방법
전위순회(preorder traversal) : VLR
- 부모노드 > 자식노드를 좌,우
중위순회(inorder traversal) : LVR
- 왼쪽 자식 > 부모노드 > 오른쪽 자식
후위순회(postorder traversal) : LRV
- 자식노드를 좌,우 > 부모노드

전위 순회
def preorder_traverse(T):
if T:
visit(T)
preorder_traverse(left[T])
preorder_traverse(right[T])
순서1 : T0 > T1 > T2
순서2: A > B D T3 > C F G
순회 순서 : A B D E H I C F G
중위 순회
def inorder_traverse(T):
if T:
inorder_traverse(left[T])
visit(T)
inorder_traverse(right[T])
순서1 : T1 > T0 > T2
순서2 : D B T3 > A > F C G
순회 순서 : D B H E I A F C G
후위 순회
def postorder_traverse(T):
if T:
postorder_traverse(left[T])
postorder_traverse(right[T])
visit(T)순서1 : T1 > T2 > T0
순서2 : D T3 B > F G C > A
순회 순서 : D H I E B F G C A

전위 순회 : A > T_B > T_C // A > B D H I E J > C F K G L M
중위 순회 : T_B > A >T_C // HDI B JE > A > FKC LGM
후위 순회 : H I D J E B K F L M G C A
이진 트리 표현- 배열
노드 번호가 i일때
부모 노드 번호 : i/2
왼쪽 자식 노드 번호 : 2*i
오른쪽 자식 노드 번호 : 2*i + 1
레벨 n의 노드 번호 시작 번호 : 2**n